[ML수업] 8주차 실습3: feature engineering- Numerical Feature Transformation (수치형)

 

### Feature Scaling

 

( #### Standardization  와  #### Min-max scaling  중 성능이 더 좋은 것 "하나만" 선택해서 진행.)

(표준화 스케일링(StandardScaler)과 Min-max 스케일링 중 어떤 것이 더 나은지는 상황에 따라 다를 수 있습니다. 어떤 스케일링 방법이 더 나은지 결정하는 요인은 데이터의 분포와 사용하는 머신러닝 모델에 따라 다를 수 있습니다. 따라서 어떤 것이 더 나은지 정확히 판단하려면 다음 사항을 고려해야 합니다:

데이터 분포: 데이터가 어떻게 분포되어 있는지를 고려해야 합니다. 표준화 스케일링은 정규 분포를 가정하고 있으므로, 데이터가 정규 분포에 가까운 경우에 더 좋은 성능을 낼 수 있습니다. 반면에 Min-max 스케일링은 데이터를 특정 범위 내로 조정하므로, 데이터의 분포와 범위에 따라 더 적합한 경우가 있을 수 있습니다.

머신러닝 모델: 사용하는 머신러닝 모델에 따라 스케일링의 영향이 다를 수 있습니다. 일부 모델은 표준화 스케일링을 선호하고, 다른 모델은 Min-max 스케일링을 선호할 수 있습니다. 예를 들어, 신경망과 같은 모델은 Min-max 스케일링을 사용하면 학습이 더 안정적으로 이루어질 수 있습니다.

데이터의 특성: 데이터에 이상치(outliers)가 있는 경우, Min-max 스케일링은 이상치에 민감할 수 있습니다. 표준화 스케일링은 이상치에 덜 영향을 받을 수 있습니다.

실험: 어떤 스케일링 방법이 더 나은지를 결정하려면 실험을 통해 검증해야 합니다. 표준화 스케일링과 Min-max 스케일링을 각각 적용한 모델을 평가하고, 모델의 성능을 비교해 보는 것이 좋습니다.)

 

(표준화 스케일링(StandardScaler)과 Min-max 스케일링을 둘 다 적용하는 것이 항상 성능을 향상시킬 것은 아닙니다. 어떤 스케일링을 적용할지는 주로 데이터의 특성과 모델의 종류에 따라 다르며, 두 가지 스케일링을 동시에 사용하는 것은 일반적으로 권장되지 않습니다. 이유는 다음과 같습니다:

중복 스케일링 문제: 표준화 스케일링과 Min-max 스케일링은 서로 다른 스케일링 방법이기 때문에, 두 가지 스케일링을 동시에 적용하면 동일한 피처에 대해 다른 스케일링 결과가 나올 수 있습니다. 이로 인해 모델이 올바르게 학습되지 않을 수 있습니다.

과적합 가능성: 두 가지 스케일링을 함께 사용하면 모델이 데이터에 더 잘 적합될 수 있지만, 이는 과적합(overfitting)의 가능성을 높일 수 있습니다. 과적합은 모델이 훈련 데이터에 너무 맞춰져서 새로운 데이터에 대한 일반화 성능이 떨어지는 현상을 의미합니다.)

 

Feature Scaling이란?

서로 다른 변수의 값 범위를 일정한 수준으로 맞추는 작업이다.

 

Feature Scaling을 하는 이유는?

1. 변수 값의 범위 또는 단위가 달라서 발생 가능한 문제를 예방할 수 있다.
2. 머신러닝 모델이 특정 데이터의 편향성을 갖는 걸 방지할 수 있다.
3. 데이터 범위 크기에 따라 모델이 학습하는 데 있어서 bias가 달라질 수 있으므로 하나의 범위 크기로 통일해주는 작업이 필요할 수 있다.

 

Feature Scaling의 종류

표준화

정규화

 

표준화 스케일링 (StandardScaler):
평균이 0이 되고, 표준 편차가 1이 되도록 스케일링합니다.
각 특성의 값이 정규 분포를 따르는 것을 가정합니다.
표준화 스케일링은 평균과 표준 편차를 사용하여 스케일링하므로 이상치(outliers)에 영향을 덜 받습니다.
대부분의 머신러닝 모델에서 사용 가능하며, 주로 평균이 0인 정규 분포를 가정하는 알고리즘에 유용합니다.

 

Min-max 스케일링:
데이터를 특정 범위(일반적으로 0에서 1)로 스케일링합니다.
모든 특성의 값이 동일한 범위 내에 있게 됩니다.
이상치에 민감할 수 있으며, 이상치가 있는 경우 스케일링 결과가 영향을 받을 수 있습니다.
주로 신경망과 같은 알고리즘에서 사용되며, 특정 범위로 값을 조정하여 모델의 학습을 안정화시키는 데 도움을 줍니다.

 

#### Standardization

# Allstate 데이터는 SVM 학습하는데 시간이 많이 소요되어 지금부터는 유방암 데이터를 사용하여 실습

from sklearn.datasets import load_breast_cancer

cancer = load_breast_cancer()
X_train, X_test, y_train, y_test = train_test_split(cancer.data, cancer.target, random_state=0) 

# Scaling 적용 전 시긱화
plt.xlim(-500, 500); plt.ylim(-500, 500)
plt.scatter(X_train[:,1], X_train[:,3], c=y_train, s=2)
plt.show()

 

스케일링 전 데이터의 분포

(x축 (X_train[:, 1]): mean texture – 유방암 조직의 질감(특징) 평균값.

y축 (X_train[:, 3]): mean area – 유방암 조직의 면적 평균값. )

 

 

스케일링 전 성능 (분류 문제에만 쓸 수 있는 두 코드)

from sklearn.svm import SVC

svm = SVC(random_state=0)
svm.fit(X_train, y_train).score(X_test, y_test)
#0.9370629370629371

 

from sklearn.tree import DecisionTreeClassifier

dt = DecisionTreeClassifier(max_depth=3, random_state=0)
dt.fit(X_train, y_train).score(X_test, y_test)
# 0.9370629370629371

 

 

위 코드는 데이터 전처리 단계에서 평균이 0이고 표준 편차가 1인 표준화(Standardization) 스케일링을 적용하는 코드입니다. (분류, 회귀 둘 다 적용 가능)

# preprocessing using zero mean and unit variance scaling
from sklearn.preprocessing import StandardScaler

scaler = StandardScaler()
X_train_sc1 = scaler.fit_transform(X_train)
X_test_sc1 = scaler.transform(X_test) # Scaling training and test data the same way

 

# Standardization 적용 후 시긱화
plt.xlim(-500, 500); plt.ylim(-500, 500)
plt.scatter(X_train_sc1[:,1], X_train_sc1[:,3], c=y_train)
plt.show()

 

svm.fit(X_train_sc1, y_train).score(X_test_sc1, y_test)
# 0.965034965034965
#성능이 향상됨

# Decision Tree를 기반으로 하는 모델은 Scaing에 거의 영향을 받지 않는다.
dt.fit(X_train_sc1, y_train).score(X_test_sc1, y_test)
#0.9370629370629371
# 성능이 그대로임

 

 

#### Min-max scaling

# preprocessing using 0-1 scaling
from sklearn.preprocessing import MinMaxScaler

scaler = MinMaxScaler()
X_train_sc2 = scaler.fit(X_train).transform(X_train)
X_test_sc2 = scaler.transform(X_test)

 

# Min-max scaling 적용 후 시긱화
plt.xlim(-500, 500); plt.ylim(-500, 500)
plt.scatter(X_train_sc2[:,1], X_train_sc2[:,3], c=y_train)
plt.show()

 

svm.fit(X_train_sc2, y_train).score(X_test_sc2, y_test)
#0.972027972027972
#성능이 더 향상됨

 

### Feature Transformation- #### Power Transformation

- 회귀 문제 연속형 데이터에 적용

파워 변환(Power Transformation)은 데이터의 분포를 변환하거나 조정하는 데이터 전처리 기법 중 하나입니다. 주로 데이터의 분포가 비대칭이거나 왜도(skewness)가 높을 때 사용되며, 데이터를 정규 분포나 균형잡힌 분포로 만들기 위해 사용됩니다.

import seaborn as sns

sns.distplot(pd.DataFrame(X_train[:,12]))
plt.show()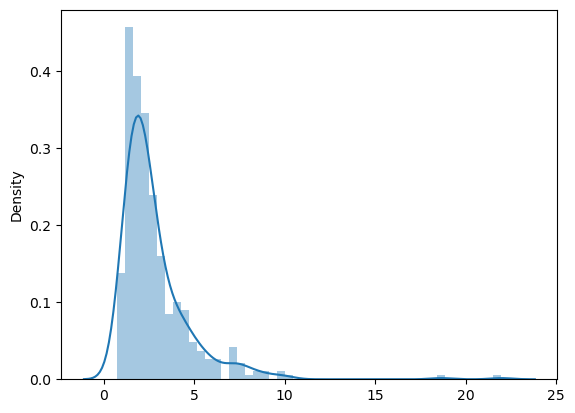

# making data more Gaussian-like
from sklearn.preprocessing import PowerTransformer

scaler = PowerTransformer(standardize=True)
X_train_sc3 = scaler.fit(X_train).transform(X_train)
X_test_sc3 = scaler.transform(X_test)

sns.distplot(pd.DataFrame(X_train_sc3[:,12]))
plt.show()

svm.fit(X_train_sc3, y_train).score(X_test_sc3, y_test)
#0.986013986013986

 

###  Binning (솔직히 잘 모르겠음)

- ""연속형 "" 데이터에 대해 열 별로 밀도 데이터를 찍어내고 낙타모양인 경우에만 적용

 

- 구간분할(Binning 또는 Discretization)은 수치형 feature를 구간별로 나누어 범주형 feature로 변환하는 방법

- 결과가 순서가 있는 범주형 feature가 되므로 순서 그대로를 수치화 하거나 OHE를 적용할 수도 있음

- 이상치 완화, 결측값처리 용이, 과적합 완화, 결과에 대한 해석 용이 등의 장점이 있으나 근본적으로는 정보손실을 초래할 수 있음.

 

- 일반적으로 구간화(빈 처리)는 연속형 데이터에 적용되는 데이터 전처리 기법입니다. 구간화는 연속형 변수를 구간(빈)으로 나누고 각 구간에 해당하는 대표값을 할당하여 연속형 변수를 이산적인 형태로 변환하는 작업을 의미합니다. 이렇게 변환된 이산형 변수는 주로 범주형 변수로 취급될 수 있습니다.

 

 

(구간화(빈 처리)는 일반적으로 회귀(regression)와 분류(classification) 문제 모두에 적용될 수 있습니다. 그러나 적용 방법과 목적은 문제 유형에 따라 다를 수 있습니다.

회귀 문제:
회귀 문제에서 구간화는 연속형 예측 변수(독립 변수)를 다룰 때 유용할 수 있습니다. 예를 들어, 주택 가격을 예측하는 회귀 모델을 고려해보겠습니다. 주택 가격은 연속형 변수이며, 이를 구간화하여 가격 대신 가격 범주(예: 저가, 중가, 고가)로 예측하는 것이 모델의 해석력을 높일 수 있습니다.

 

분류 문제:
분류 문제에서도 구간화를 적용할 수 있지만, 주로 연속형 특성을 범주형 특성으로 변환하는 데 사용됩니다. 예를 들어, 나이라는 연속형 특성을 연령대(예: 어린이, 청소년, 성인)로 구간화하여 분류 모델에 적용할 수 있습니다.
구간화는 데이터를 더 이해하기 쉽게 만들거나 모델의 해석력을 높이기 위해 사용되며, 문제 유형에 따라 어떻게 적용할지 결정됩니다. 따라서 구간화는 회귀와 분류 문제 모두에 적용될 수 있으며, 적절한 방식으로 적용하는 것이 중요합니다.)

 

 

데이터셋 X_train_sc3에서 7번째 열(특성)에 해당하는 데이터를 선택한 것입니다. 이 특성에 대한 밀도 플롯을 생성하고 시각적으로 표시합니다.

#비닝: 인코딩과 반대로 수치형을 범주형으로 나누는거
#아래그래프처럼 낙타 혹이 여러 개 있는 분포가 비닝을 적용하면 좋은 분포임.


sns.kdeplot(X_train_sc3[:,7])
plt.show()

 

 이 코드는 주어진 데이터의 특정 열을 지정된 구간 수로 나누어 이산화하는 작업을 수행하며, 이산화된 구간의 경계값을 확인할 수 있습니다.

from sklearn.preprocessing import KBinsDiscretizer

bin_cols = [7]

X_train_sc3_bin = X_train_sc3.copy()
X_test_sc3_bin = X_test_sc3.copy()

### K-bins discretization
# - encode: 'onehot', 'onehot-dense', 'ordinal'
# - strategy: 'uniform', 'quantile' , 'kmeans'

# 순서 그대로를 수치화
#젤 중요한 변수 : n_bins=5,
#인코딩 방법: 순서 있으면 ordinal, 순서 없으면 원핫이 좋음
bin = KBinsDiscretizer(n_bins=5, encode='ordinal', strategy='uniform')
X_train_sc3_bin[:,bin_cols] = bin.fit_transform(X_train_sc3[:,bin_cols])
X_test_sc3_bin[:,bin_cols] = bin.transform(X_test_sc3[:,bin_cols])

bin.bin_edges_
'''
array([array([-1.89375698, -1.08996257, -0.28616817,  0.51762624,  1.32142065,
               2.12521506])                                                   ],
      dtype=object)
'''

 

이 코드는 주어진 데이터에 대해 K-bins 이산화(K-bins discretization)를 수행하고, 그 결과에 원-핫 인코딩(One-Hot Encoding)을 적용하는 작업을 수행합니다.

X_train_sc3_bin = X_train_sc3.copy()
X_test_sc3_bin = X_test_sc3.copy()

# OHE 적용
bin = KBinsDiscretizer(n_bins=5, encode='onehot-dense', strategy='uniform')
X_train_sc3_bin = np.c_[np.delete(X_train_sc3,bin_cols,axis=1), bin.fit_transform(X_train_sc3[:,bin_cols])]
X_test_sc3_bin = np.c_[np.delete(X_test_sc3,bin_cols,axis=1), bin.transform(X_test_sc3[:,bin_cols])]

X_train_sc3_bin.shape, X_train_sc3.shape

svm.fit(X_train_sc3_bin, y_train).score(X_test_sc3_bin, y_test)
#0.986013986013986

sns.kdeplot(X_train_sc3_bin[:,7])
plt.show()